Neutron scattering spectroscopy for dynamics
Probing single-particle dynamics is central to the study of atomic and molecular motion across many areas of research. These dynamics can be fully described by the van Hove self-distribution function, G_self(r,t), which represents the probability that a species has diffused a distance r over time t, or equivalently, by its spatial Fourier transform, I(Q,t), known as intermediate scattering function. Current neutron-scattering spectroscopies for measuring these dynamics rely on the exchanged energy of each scattered neutron as shown by Bertram N. Brockhouse 1994 Physics Nobel Laureate. Rather than these “inverse” approaches, we have recently proposed an alternative approach that uses the portion of neutrons scattered into the elastic line within different observation times that can be scanned by varying the energy band-width of the neutron package fired into the sample (Fig. 1). This new approach is based on the observation we recently made that the measured elastic scattering intensity corresponds to the running time-integral of I(t), weighted by the incoming neutron energy distribution, up to a time inversely proportional to the selected energy band-width (Fig. 2). It turned out that our new method has a number advantages in comparison to quasi-elastic neutron scattering - the standard method for dynamics - as it has 100-times more counts at the detector which transforms into a 10-times better statistical significance at the I(t)-level (Fig. 3). The method was also successfully tested in practice on the high-resolution spectrometer IN16B at the Institute Laue-Langevin in Grenoble, France (Fig. 4) operated both in QENS and vHI modes (Fig. 5). More recently, we present a new "elastic" method for measuring dynamics using an oscillating cosine-like energy-distribution neutron-package at the sample and measure solely the portion scattered into the elastic line. This portion corresponds to elastically scattered neutrons and, in addition, inelastic components that are scattered with a probability directly proportional to the cosine Fourier-coefficients of the exchanged-energy spectrum. The counts at the detector thus correspond to the van Hove intermediate scattering function. We denote this new method as “Fourier transform neutron scattering” (FTNS).
the realization of such a concept is investigated using an oscillating incident beam produced via a precession method and a secondary spectrometer identical to a BS instrument using crystal analyzers. The instrument is denoted “Modulated Intensity with Diffraction Analysis Spectrometer” (MIDAS). However, simpler approaches, e.g., choppers, may also be used for an FTNS instrument.
the realization of such a concept is investigated using an oscillating incident beam produced via a precession method and a secondary spectrometer identical to a BS instrument using crystal analyzers. The instrument is denoted “Modulated Intensity with Diffraction Analysis Spectrometer” (MIDAS). However, simpler approaches, e.g., choppers, may also be used for an FTNS instrument.
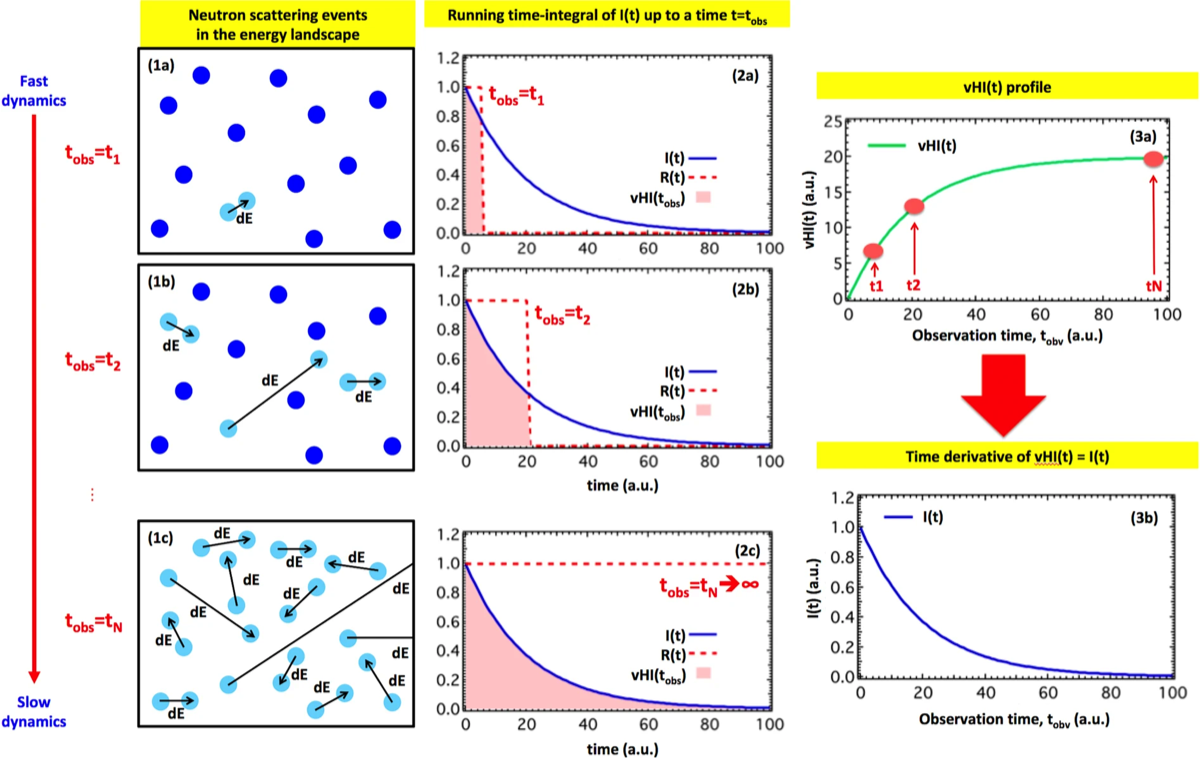
Fig. 1 - Illustration of the concept. Column 1 sketches the energy landscape of a system of particles, at three different observation times, t_obs. t_obs is the time-resolution of the measurement and is inversely proportional to the energy band-width allowed into the sample, also known as instrumental energy-resolution of the primary spectrometer. At short t_obs only the rapid motions are detected, most of the system appearing at rest (1a). At intermediate t_obs other motions are detected (1b), and for long t_obs the slower motions are also detected (1c). Existing techniques require determination of many exchanged energy values, ΔE, to access I(t), typically operating at fixed t_obs. In general, our approach of obtaining the proportion of particles “at rest”, as a function of t_obs, should be more efficient. This proportion formally corresponds to the running time-integral of I(t), that is the van Hove integral vHI(t = t_obs), as sketched in column 2, in which each t_obs determines the upper integration limit of I(t). Differentiation of the measured vHI(t) (3a) provides I(t) directly (3b). Even though numerical differentiation can work, there are other robust methods to compute it, including the polynomial method in the powers of time we developed, see next figure. Taken from our Sci Rep 2019
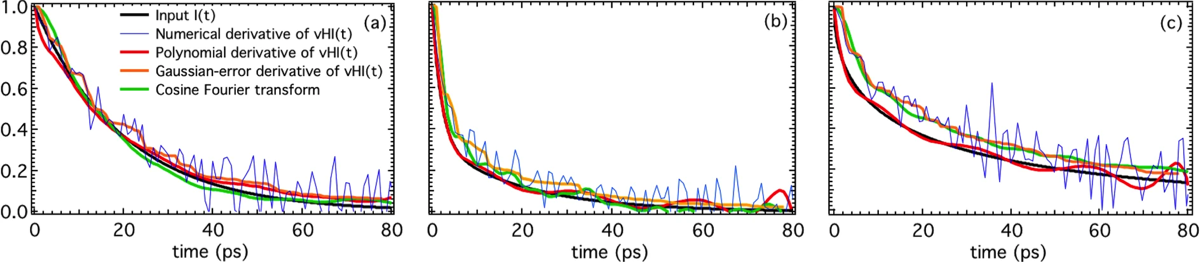
Fig. 2 - Numerical validation with counting error of several approaches to obtain I(t) from the “experimental” vHI(t). The three plots are: (a) single exponential, (b) double exponential, and (c) stretched exponential. The numerical derivative of vHI(t) is intractable, but its polynomial derivative and Gaussian-error derivative reproduce the input function well. The cosine FT is also shown for a consistency check. Taken from our Sci Rep 2019
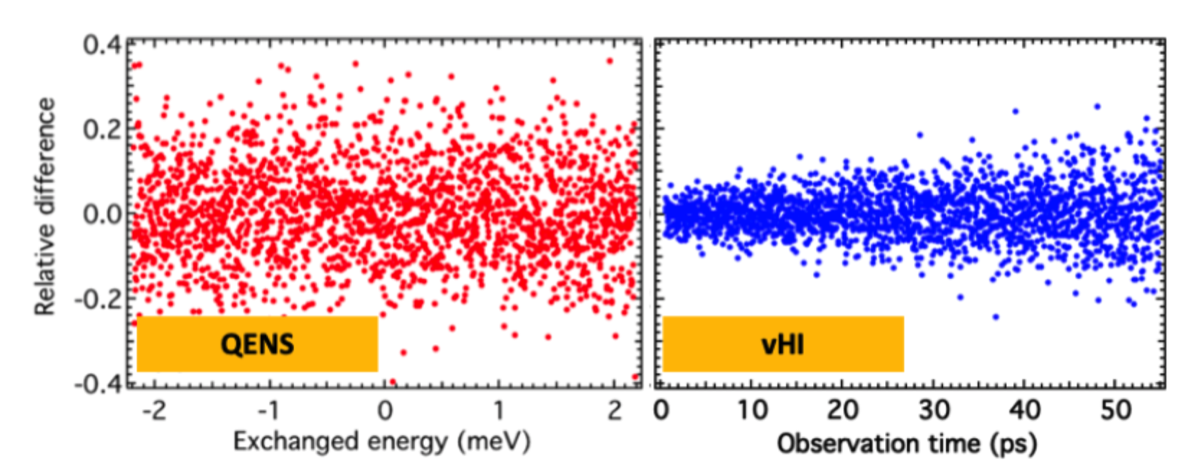
Fig. 3 - Relative difference between “standard” and “perfect” outputs for (a) quasi-elastic neutron scattering (QENS) and (b) van Hove Integral neutron spectroscopy (vHI). These results were obtained by a numerical Monte-Carlo simulation with McStas of an instrument that is equally capable of measuring QENS and vHI under identical conditions. Firstly, at the raw-data level vHI achieves 100 times more neutrons at the detector than QENS. Secondly, vHI has a factor of 2 less statistical error, which would translate to an overall gain of 4 for vHI in counting-time. Lastly, we compare the distortions caused in obtaining the final I(t) via time-Fourier transform (QENS) and polynomial time-derivative (vHI). Here, the statistical error is 10 times smaller for vHI. This last comparison is the most important result where the 10 times smaller residual for vHI gives a net gain in counting time of 100 better than QENS to obtain the same underlying dynamics of the system under study. Taken from our Sci Rep 2020
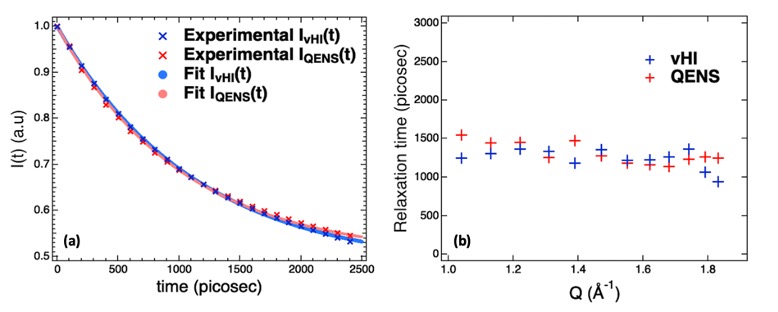
Fig. 4 - Experimental validation on IN16B at the Institute Laue-Langevin, Grenoble, France. The intermediate scattering functions, I(Q,t), in panel (a) and the relaxation times versus Q in panel (b) obtained by the two methods — vHI and QENS — are strikingly similar providing a direct experimental validation of the vHI method. Perhaps surprisingly, the counting statistics of the two methods are comparable even though the instrument used was expressly designed for QENS. This shows that the methodology modification adopted here can be used in practice to access vHI profiles at many of the backscattering spectrometers worldwide. We also show that partial integrations of the measured QENS spectrum cannot provide the vHI profile, which clarifies a common misconception. Taken from our Sci Rep 2021

Fig. 5 - The most general layout and modus operandi of a neutron backscattering spectrometer in which the interplay between the primary and the secondary spectrometers enables the measurement of either the QENS spectrum or the vHI profile. QENS needs to compute the energy exchange due to the scattering process and thus operates in the “inelastic” regime with fixed energy resolution. vHI is fundamentally different, it operates in the purely “elastic” regime. For both QENS and vHI there are three constant quantitates and one variable. Here, for QENS, dE1, dE2 and E2 are constant and E1 is varied (with, usually, dE1 = dE2). For vHI, instead, E1, E2 and dE2 are constant and dE1 is varied. Basically, in practice, we varied the neutron-energy band-widths incident at the sample via a step-wise variation of the frequency of the monochromator Doppler-drive. This provides a measurement of the vHI profile at the detectors. Taken from our Sci Rep 2021
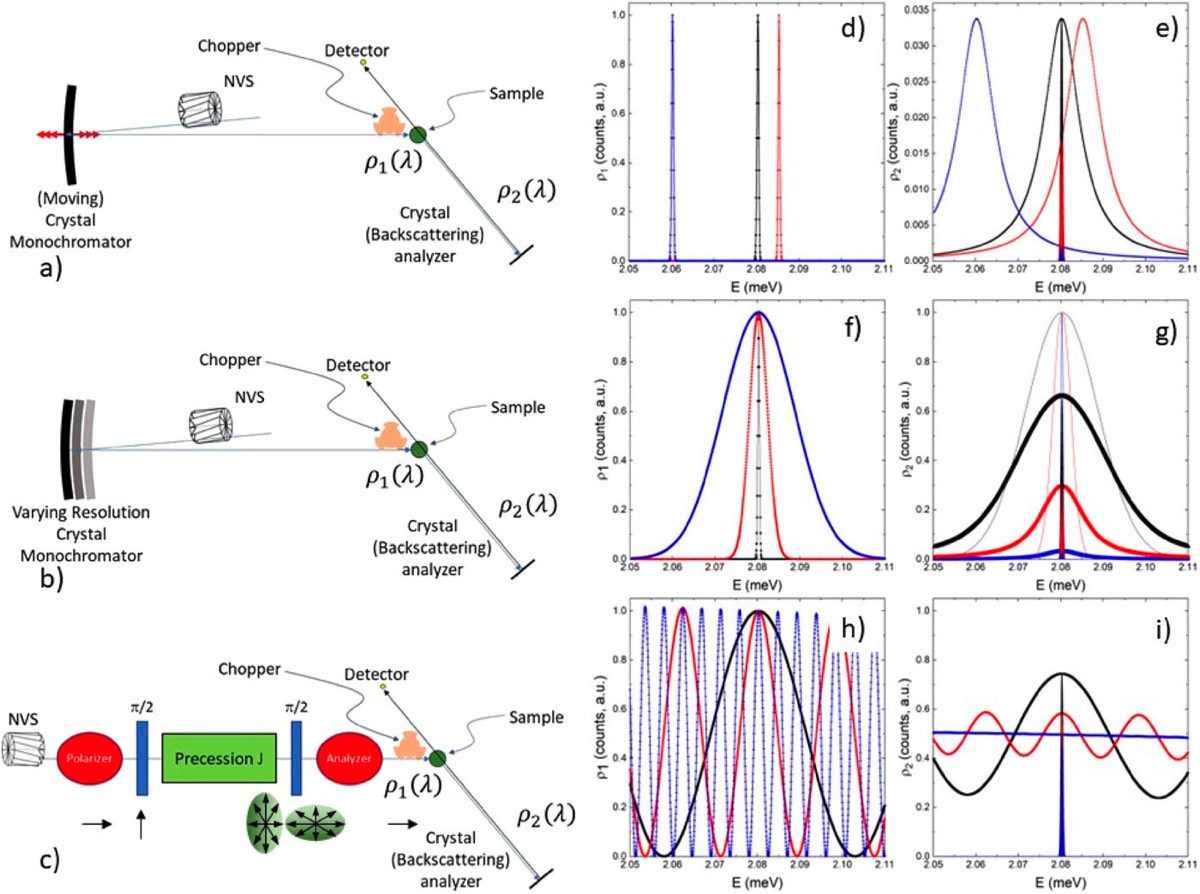
Fig. 6 - Diagrams showing the layout and operation of a standard back-scattering (BS), our vHI, and our new FTNS spectrometers, respectively, in (a), (b) and (c). In (d), (f), and (h), the wavelength distribution of the incoming neutron beam for the three instrument configurations with Si (111) crystal analysers is reported. In (e), (g), and (i), the wavelength distribution of the scattered neutron beam for the three instrument configurations is reported; the shaded areas around E = 2.0803 meV represent the neutrons selected using the analysers, which reach the detector. Taken from our Rev Sci Instrum 2024
Selected publications:
Conceptual study of a new instrument for dynamic neutron scattering measurements – The modulated intensity with diffraction analysis spectrometer (MIDAS)
A. Benedetto, G. Kearley, A. Faraone, Review of Scientific Instruments, 95, 043901, (2024)
>>>> LINK TO THE PAPER <<<<
A. Benedetto, G. Kearley, A. Faraone, Review of Scientific Instruments, 95, 043901, (2024)
>>>> LINK TO THE PAPER <<<<
Experimental demonstration of the novel “van-Hove integral method (vHI)” for measuring diffusive dynamics by elastic neutron scattering
A. Benedetto and G.J. Kearley, Scientific Reports, 11, 14093, (2021)
>>>> LINK TO THE PAPER <<<<
A. Benedetto and G.J. Kearley, Scientific Reports, 11, 14093, (2021)
>>>> LINK TO THE PAPER <<<<
A Quantitative Comparison of the Counting Significance of van Hove Integral Spectroscopy and Quasielastic Neutron Scattering
A. Benedetto and G.J. Kearley, Scientific Reports, 10, 6350, (2020)
>>>> LINK TO THE PAPER <<<<
A. Benedetto and G.J. Kearley, Scientific Reports, 10, 6350, (2020)
>>>> LINK TO THE PAPER <<<<
Dynamics from elastic neutron-scattering via direct measurement of the running time-integral of the van Hove distribution function
A. Benedetto and G.J. Kearley, Scientific Reports, 9, 11284, (2019)
>>>> LINK TO THE PAPER <<<<
A. Benedetto and G.J. Kearley, Scientific Reports, 9, 11284, (2019)
>>>> LINK TO THE PAPER <<<<
Elastic Scattering Spectroscopy (ESS): an Instrument-Concept for Dynamics of Complex (Bio-) Systems from Elastic Scattering
A. Benedetto and G.J. Kearley, Scientific Reports, 6, 34266, (2016)
>>>> LINK TO THE PAPER <<<<
A. Benedetto and G.J. Kearley, Scientific Reports, 6, 34266, (2016)
>>>> LINK TO THE PAPER <<<<
Elastic Incoherent Neutron Scattering Operating by Varying Instrumental Energy Resolution: Principle, Simulations and Experiments of the Resolution Elastic Neutron Scattering (RENS)
S. Magazù, F. Migliardo, A. Benedetto, Review of Scientific Instruments, 82, 105115, (2011)
>>>> LINK TO THE PAPER <<<<
S. Magazù, F. Migliardo, A. Benedetto, Review of Scientific Instruments, 82, 105115, (2011)
>>>> LINK TO THE PAPER <<<<